Intersection of F Is a Subset of the Union of F for All Family of Sets F

This article is about what mathematicians call "intuitive" or "naive" fix theory. For a more than detailed account, see Naive set theory. For a rigorous modern axiomatic treatment of sets, encounter Set theory.

Drove of mathematical objects

A set is the mathematical model for a collection of different^[1] things;^{[2] [three] [four]} a ready contains elements or members, which can be mathematical objects of any kind: numbers, symbols, points in space, lines, other geometrical shapes, variables, or even other sets.^[5] The prepare with no element is the empty set; a set with a single element is a singleton. A prepare may have a finite number of elements or be an infinite set up. Two sets are equal if they take precisely the same elements.^{[half dozen]}

Sets are ubiquitous in modernistic mathematics. Indeed, ready theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the outset half of the 20th century.^[5]

Origin [edit]

The concept of a gear up emerged in mathematics at the end of the 19th century.^[seven] The German word for ready, Menge, was coined past Bernard Bolzano in his work Paradoxes of the Infinite.^{[eight] [9] [10]}

Passage with a translation of the original ready definition of Georg Cantor. The High german discussion Menge for fix is translated with aggregate here.

Georg Cantor, 1 of the founders of gear up theory, gave the following definition at the beginning of his Beiträge zur Begründung der transfiniten Mengenlehre:^[1]

A prepare is a gathering together into a whole of definite, distinct objects of our perception or our thought—which are chosen elements of the set.

Bertrand Russell chosen a set a course:^[eleven]

When mathematicians deal with what they phone call a manifold, aggregate, Menge, ensemble, or some equivalent proper name, it is mutual, peculiarly where the number of terms involved is finite, to regard the object in question (which is in fact a course) as defined past the enumeration of its terms, and as consisting possibly of a single term, which in that case is the class.

Naive prepare theory [edit]

The foremost property of a prepare is that it can take elements, also called members. 2 sets are equal when they take the same elements. More than precisely, sets A and B are equal if every element of A is an element of B, and every element of B is an element of A; this property is called the extensionality of sets.^[12]

The unproblematic concept of a set has proved enormously useful in mathematics, but paradoxes ascend if no restrictions are placed on how sets can be constructed:

• Russell's paradox shows that the "set up of all sets that practice not contain themselves", i.e., {x | x is a set and x ∉ 10}, cannot exist.
• Cantor'south paradox shows that "the gear up of all sets" cannot be.

Naïve set theory defines a set as any well-defined collection of distinct elements, but problems ascend from the vagueness of the term well-divers.

Axiomatic set theory [edit]

In subsequent efforts to resolve these paradoxes since the fourth dimension of the original formulation of naïve set theory, the properties of sets have been defined past axioms. Axiomatic set theory takes the concept of a set as a primitive notion.^[thirteen] The purpose of the axioms is to provide a basic framework from which to deduce the truth or falsity of detail mathematical propositions (statements) about sets, using first-gild logic. According to Gödel's incompleteness theorems yet, information technology is not possible to use first-guild logic to prove any such particular axiomatic set theory is free from paradox.^{[ citation needed ]}

How sets are defined and set notation [edit]

Mathematical texts commonly denote sets by capital letter messages^{[xiv] [five]} in italic, such every bit A, B, C.^[fifteen] A set may besides be called a collection or family, especially when its elements are themselves sets.

Roster notation [edit]

Roster or enumeration notation defines a set by listing its elements between curly brackets, separated by commas:^{[sixteen] [17] [18] [nineteen]}

A = {4, 2, 1, iii}

B = {blueish, white, red}.

In a set, all that matters is whether each element is in it or not, so the ordering of the elements in roster notation is irrelevant (in contrast, in a sequence, a tuple, or a permutation of a set up, the ordering of the terms matters). For example, {2, four, 6} and {4, half-dozen, 4, 2} represent the aforementioned set.^{[20] [15] [21]}

For sets with many elements, specially those following an implicit pattern, the list of members tin can be abbreviated using an ellipsis '...'.^{[22] [23]} For instance, the set of the beginning thousand positive integers may exist specified in roster notation every bit

{one, 2, iii, ..., 1000}.

Infinite sets in roster annotation [edit]

An infinite set is a set with an endless list of elements. To describe an infinite set in roster notation, an ellipsis is placed at the finish of the listing, or at both ends, to indicate that the list continues forever. For example, the set of nonnegative integers is

{0, 1, 2, 3, four, ...},

and the fix of all integers is

{..., −3, −2, −ane, 0, 1, 2, three, ...}.

Semantic definition [edit]

Another way to ascertain a set is to use a rule to determine what the elements are:

Let A be the set whose members are the first four positive integers.

Let B be the gear up of colors of the French flag.

Such a definition is called a semantic description.^{[24] [25]}

Ready-builder notation [edit]

Set-builder notation specifies a set as a selection from a larger ready, determined by a condition on the elements.^{[25] [26] [27]} For example, a fix F tin be divers every bit follows:

F ${\displaystyle =\{due north\mid due north{\text{ is an integer, and }}0\leq north\leq 19\}.}$

In this annotation, the vertical bar "|" means "such that", and the description can be interpreted equally "F is the set of all numbers n such that northward is an integer in the range from 0 to 19 inclusive". Some authors use a colon ":" instead of the vertical bar.^[28]

Classifying methods of definition [edit]

Philosophy uses specific terms to classify types of definitions:

• An intensional definition uses a rule to determine membership. Semantic definitions and definitions using set-architect notation are examples.
• An extensional definition describes a set by listing all its elements.^[25] Such definitions are besides chosen enumerative.
• An ostensive definition is one that describes a gear up by giving examples of elements; a roster involving an ellipsis would be an instance.

Membership [edit]

If B is a set and x is an element of B, this is written in shorthand equally x ∈ B , which can also be read as "10 belongs to B", or "10 is in B".^[12] The statement "y is non an element of B" is written as y ∉ B , which can also exist read every bit or "y is non in B".^{[29] [30]}

For example, with respect to the sets A = {ane, 2, 3, iv}, B = {bluish, white, ruby-red}, and F = {n | n is an integer, and 0 ≤ due north ≤ xix},

iv ∈ A and 12 ∈ F ; and

20 ∉ F and green ∉ B .

The empty set [edit]

The empty set up (or null set) is the unique set that has no members. It is denoted ∅ or ${\displaystyle \emptyset }$ or { }^{[31] [32]} or ϕ ^[33] (or ϕ).^[34]

Singleton sets [edit]

A singleton set is a fix with exactly one element; such a gear up may also exist called a unit set.^{[half dozen]} Any such set can be written every bit {x}, where x is the element. The set {x} and the element ten mean unlike things; Halmos^[35] draws the analogy that a box containing a hat is non the same as the chapeau.

Subsets [edit]

If every element of set A is also in B, and then A is described as being a subset of B, or contained in B, written A ⊆ B,^[36] or B ⊇ A.^[37] The latter notation may be read B contains A, B includes A, or B is a superset of A. The relationship between sets established by ⊆ is called inclusion or containment. 2 sets are equal if they contain each other: A ⊆ B and B ⊆ A is equivalent to A = B.^[26]

If A is a subset of B, but A is not equal to B, then A is called a proper subset of B. This can be written A ⊊ B. Likewise, B ⊋ A means B is a proper superset of A, i.eastward. B contains A, and is non equal to A.

A third pair of operators ⊂ and ⊃ are used differently by dissimilar authors: some authors use A ⊂ B and B ⊃ A to hateful A is any subset of B (and not necessarily a proper subset),^{[38] [29]} while others reserve A ⊂ B and B ⊃ A for cases where A is a proper subset of B.^[36]

Examples:

• The set of all humans is a proper subset of the set of all mammals.
• {1, 3} ⊂ {i, 2, 3, 4}.
• {1, ii, 3, 4} ⊆ {1, two, three, iv}.

The empty set is a subset of every set,^[31] and every ready is a subset of itself:^[38]

• ∅ ⊆ A.
• A ⊆ A.

Euler and Venn diagrams [edit]

A is a subset of B.
B is a superset of A.

An Euler diagram is a graphical representation of a collection of sets; each set is depicted as a planar region enclosed past a loop, with its elements inside. If A is a subset of B, then the region representing A is completely inside the region representing B. If two sets have no elements in common, the regions exercise non overlap.

A Venn diagram, in dissimilarity, is a graphical representation of due north sets in which the n loops carve up the aeroplane into 2 ⁿ zones such that for each manner of selecting some of the n sets (perhaps all or none), in that location is a zone for the elements that belong to all the selected sets and none of the others. For example, if the sets are A, B, and C, there should exist a zone for the elements that are within A and C and outside B (even if such elements do not exist).

Special sets of numbers in mathematics [edit]

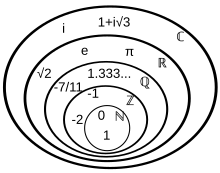
In that location are sets of such mathematical importance, to which mathematicians refer and then frequently, that they have caused special names and notational conventions to identify them.

Many of these of import sets are represented in mathematical texts using bold (e.chiliad. ${\displaystyle {\mathbf {Z}}}$ ) or blackboard assuming (e.one thousand. ${\displaystyle \mathbb {Z} }$ ) typeface.^[39] These include

• ${\displaystyle {\mathbf {Northward}}}$ or ${\displaystyle \mathbb {Due north} }$ , the set of all natural numbers: ${\displaystyle {\mathbf {N}}=\{0,1,2,3,...\}}$ (often, authors exclude 0);^[39]
• ${\displaystyle {\mathbf {Z}}}$ or ${\displaystyle \mathbb {Z} }$ , the prepare of all integers (whether positive, negative or zero): ${\displaystyle {\mathbf {Z}}=\{...,-ii,-1,0,1,2,three,...\}}$ ;^[39]
• ${\displaystyle {\mathbf {Q}}}$ or ${\displaystyle \mathbb {Q} }$ , the set of all rational numbers (that is, the set of all proper and improper fractions): ${\displaystyle {\mathbf {Q}}=\left\{{\frac {a}{b}}\mid a,b\in {\mathbf {Z}},b\neq 0\correct\}}$ . For example, − vii / four ∈ Q and v = five / i ∈ Q ;^[39]
• ${\displaystyle {\mathbf {R}}}$ or ${\displaystyle \mathbb {R} }$ , the set of all real numbers, including all rational numbers and all irrational numbers (which include algebraic numbers such as ${\displaystyle {\sqrt {ii}}}$ that cannot be rewritten as fractions, every bit well as transcendental numbers such equally π and east );^[39]
• ${\displaystyle {\mathbf {C}}}$ or ${\displaystyle \mathbb {C} }$ , the set of all complex numbers: C = {a + bi | a, b ∈ R}, for case, one + 2i ∈ C .^[39]

Each of the in a higher place sets of numbers has an infinite number of elements. Each is a subset of the sets listed below it.

Sets of positive or negative numbers are sometimes denoted past superscript plus and minus signs, respectively. For example, ${\displaystyle \mathbf {Q} ^{+}}$ represents the set of positive rational numbers.

Functions [edit]

A part (or mapping) from a set A to a prepare B is a rule that assigns to each "input" element of A an "output" that is an element of B; more formally, a function is a special kind of relation, one that relates each chemical element of A to exactly one element of B. A role is called

• injective (or one-to-ane) if it maps any ii different elements of A to dissimilar elements of B,
• surjective (or onto) if for every element of B, there is at to the lowest degree one element of A that maps to it, and
• bijective (or a one-to-1 correspondence) if the function is both injective and surjective — in this case, each element of A is paired with a unique element of B, and each chemical element of B is paired with a unique chemical element of A, then that there are no unpaired elements.

An injective office is called an injection, a surjective role is chosen a surjection, and a bijective office is chosen a bijection or one-to-i correspondence.

Cardinality [edit]

The cardinality of a set S , denoted | S |, is the number of members of South .^[twoscore] For case, if B = {blueish, white, red}, and then |B| = 3. Repeated members in roster notation are non counted,^{[41] [42]} so |{bluish, white, red, blue, white}| = 3, too.

More formally, two sets share the same cardinality if there exists a one-to-one correspondence between them.

The cardinality of the empty set is zero.^[43]

Infinite sets and infinite cardinality [edit]

The list of elements of some sets is endless, or infinite. For example, the set ${\displaystyle \mathbb {N} }$ of natural numbers is infinite.^[26] In fact, all the special sets of numbers mentioned in the section to a higher place, are infinite. Infinite sets have infinite cardinality.

Some infinite cardinalities are greater than others. Arguably i of the most significant results from set theory is that the gear up of real numbers has greater cardinality than the set of natural numbers.^[44] Sets with cardinality less than or equal to that of ${\displaystyle \mathbb {Due north} }$ are called countable sets; these are either finite sets or countably infinite sets (sets of the same cardinality as ${\displaystyle \mathbb {N} }$ ); some authors use "countable" to mean "countably space". Sets with cardinality strictly greater than that of ${\displaystyle \mathbb {N} }$ are called uncountable sets.

However, it can be shown that the cardinality of a straight line (i.e., the number of points on a line) is the aforementioned as the cardinality of any segment of that line, of the entire aeroplane, and indeed of any finite-dimensional Euclidean space.^[45]

The Continuum Hypothesis [edit]

The Continuum Hypothesis, formulated by Georg Cantor in 1878, is the statement that there is no ready with cardinality strictly betwixt the cardinality of the natural numbers and the cardinality of a straight line.^[46] In 1963, Paul Cohen proved that the Continuum Hypothesis is contained of the axiom arrangement ZFC consisting of Zermelo–Fraenkel set theory with the axiom of pick.^[47] (ZFC is the most widely-studied version of evident set theory.)

Power sets [edit]

The power set of a set up South is the set of all subsets of S .^[26] The empty fix and South itself are elements of the ability prepare of S , because these are both subsets of South . For example, the ability fix of {i, 2, iii} is {∅, {1}, {ii}, {iii}, {i, ii}, {1, 3}, {2, 3}, {1, 2, iii}}. The ability gear up of a set S is commonly written as P(S) or two ^S .^{[26] [48] [fifteen]}

If South has n elements, then P(S) has 2 ^northward elements.^[49] For case, {1, 2, 3} has 3 elements, and its power set up has 2³ = 8 elements, as shown above.

If Due south is infinite (whether countable or uncountable), so P(Southward) is uncountable. Moreover, the power fix is e'er strictly "bigger" than the original set, in the sense that any attempt to pair upward the elements of Southward with the elements of P(Due south) will exit some elements of P(Southward) unpaired. (In that location is never a bijection from S onto P(S).)^[50]

Partitions [edit]

A partition of a set Southward is a set of nonempty subsets of S, such that every element 10 in S is in exactly one of these subsets. That is, the subsets are pairwise disjoint (pregnant any two sets of the partition contain no chemical element in mutual), and the union of all the subsets of the partition is Due south.^{[51] [52]}

Basic operations [edit]

There are several key operations for amalgam new sets from given sets.

Unions [edit]

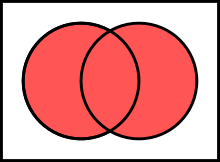
The marriage of A and B , denoted A ∪ B

Ii sets can be joined: the union of A and B , denoted by A ∪ B , is the prepare of all things that are members of A or of B or of both.

Examples:

• {1, 2} ∪ {one, 2} = {1, two}.
• {ane, 2} ∪ {2, 3} = {ane, 2, 3}.
• {1, 2, iii} ∪ {three, four, 5} = {one, ii, 3, iv, 5}.

Some basic backdrop of unions:

• A ∪ B = B ∪ A.
• A ∪ (B ∪ C) = (A ∪ B) ∪ C.
• A ⊆ (A ∪ B).
• A ∪ A = A.
• A ∪ ∅ = A.
• A ⊆ B if and only if A ∪ B = B.

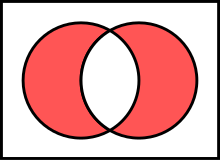
Intersections [edit]

A new set tin likewise be constructed by determining which members two sets have "in common". The intersection of A and B, denoted by A ∩ B, is the set of all things that are members of both A and B. If A ∩ B = ∅, then A and B are said to exist disjoint.

The intersection of A and B, denoted A ∩ B.

Examples:

• {one, 2} ∩ {1, ii} = {1, 2}.
• {1, 2} ∩ {ii, iii} = {ii}.
• {1, ii} ∩ {3, 4} = ∅.

Some basic backdrop of intersections:

• A ∩ B = B ∩ A.
• A ∩ (B ∩ C) = (A ∩ B) ∩ C.
• A ∩ B ⊆ A.
• A ∩ A = A.
• A ∩ ∅ = ∅.
• A ⊆ B if and just if A ∩ B = A.

Complements [edit]

The relative complement
of B in A

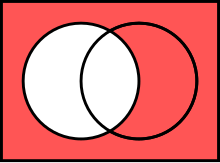
The symmetric difference of A and B

Ii sets can also exist "subtracted". The relative complement of B in A (too called the fix-theoretic deviation of A and B), denoted past A \ B (or A − B ), is the set of all elements that are members of A, but not members of B. It is valid to "subtract" members of a set that are not in the set, such as removing the element dark-green from the set {one, ii, three}; doing and so will not affect the elements in the fix.

In certain settings, all sets under word are considered to be subsets of a given universal set U. In such cases, U \ A is called the absolute complement or simply complement of A, and is denoted by A′ or A^c.

• A′ = U \ A

Examples:

• {1, 2} \ {1, two} = ∅.
• {1, 2, iii, 4} \ {ane, 3} = {2, 4}.
• If U is the set up of integers, E is the set of even integers, and O is the set of odd integers, then U \ E = E′ = O.

Some bones properties of complements include the following:

• A \ B ≠ B \ A for A ≠ B .
• A ∪ A′ = U.
• A ∩ A′ = ∅.
• (A′)′ = A.
• ∅ \ A = ∅.
• A \ ∅ = A.
• A \ A = ∅.
• A \ U = ∅.
• A \ A′ = A and A′ \ A = A′.
• U′ = ∅ and ∅′ = U.
• A \ B = A ∩ B′.
• if A ⊆ B then A \ B = ∅.

An extension of the complement is the symmetric difference, defined for sets A, B as

${\displaystyle A\,\Delta \,B=(A\setminus B)\loving cup (B\setminus A).}$

For example, the symmetric divergence of {seven, 8, 9, 10} and {9, x, eleven, 12} is the fix {7, 8, 11, 12}. The ability fix of any set becomes a Boolean ring with symmetric difference equally the add-on of the ring (with the empty fix as neutral element) and intersection as the multiplication of the ring.

Cartesian product [edit]

A new set can be constructed by associating every element of i set with every element of another set. The Cartesian product of two sets A and B, denoted past A × B, is the set of all ordered pairs (a, b) such that a is a member of A and b is a member of B.

Examples:

• {1, 2} × {ruby-red, white, green} = {(1, ruddy), (1, white), (1, greenish), (2, cherry-red), (2, white), (2, green)}.
• {1, 2} × {one, 2} = {(i, 1), (1, two), (2, i), (2, ii)}.
• {a, b, c} × {d, e, f} = {(a, d), (a, e), (a, f), (b, d), (b, e), (b, f), (c, d), (c, e), (c, f)}.

Some basic properties of Cartesian products:

• A × ∅ = ∅.
• A × (B ∪ C) = (A × B) ∪ (A × C).
• (A ∪ B) × C = (A × C) ∪ (B × C).

Allow A and B be finite sets; then the cardinality of the Cartesian product is the production of the cardinalities:

• |A × B| = |B × A| = |A| × |B|.

Applications [edit]

Sets are ubiquitous in modern mathematics. For example, structures in abstract algebra, such as groups, fields and rings, are sets closed under one or more operations.

I of the chief applications of naive set theory is in the construction of relations. A relation from a domain A to a codomain B is a subset of the Cartesian product A × B . For example, because the set Due south = {rock, paper, pair of scissors} of shapes in the game of the aforementioned name, the relation "beats" from S to South is the ready B = {(scissors,paper), (paper,stone), (stone,scissors)}; thus ten beats y in the game if the pair (ten,y) is a member of B . Another example is the set F of all pairs (x, x ²), where 10 is real. This relation is a subset of R × R , considering the prepare of all squares is subset of the set of all existent numbers. Since for every 10 in R , i and simply one pair (10,...) is constitute in F , it is chosen a role. In functional notation, this relation can exist written equally F(x) = x ^two .

Principle of inclusion and exclusion [edit]

The inclusion-exclusion principle is used to calculate the size of the union of sets: the size of the matrimony is the size of the two sets, minus the size of their intersection.

The inclusion–exclusion principle is a counting technique that tin be used to count the number of elements in a union of two sets—if the size of each set up and the size of their intersection are known. Information technology tin be expressed symbolically as

${\displaystyle |A\cup B|=|A|+|B|-|A\cap B|.}$

A more full general course of the principle tin can be used to observe the cardinality of any finite wedlock of sets:

${\displaystyle {\brainstorm{aligned}\left|A_{1}\cup A_{2}\loving cup A_{3}\cup \ldots \cup A_{n}\right|=&\left(\left|A_{one}\right|+\left|A_{two}\correct|+\left|A_{3}\right|+\ldots \left|A_{n}\correct|\right)\\&{}-\left(\left|A_{i}\cap A_{two}\right|+\left|A_{1}\cap A_{3}\correct|+\ldots \left|A_{north-one}\cap A_{n}\right|\right)\\&{}+\ldots \\&{}+\left(-1\correct)^{n-ane}\left(\left|A_{1}\cap A_{2}\cap A_{3}\cap \ldots \cap A_{n}\right|\right).\finish{aligned}}}$

De Morgan'southward laws [edit]

Augustus De Morgan stated two laws about sets.

If A and B are any two sets then,

• (A ∪ B)′ = A′ ∩ B′

The complement of A union B equals the complement of A intersected with the complement of B.

• (A ∩ B)′ = A′ ∪ B′

The complement of A intersected with B is equal to the complement of A union to the complement of B.

See also [edit]

• Algebra of sets
• Alternative set theory
• Category of sets
• Class (gear up theory)
• Dumbo prepare
• Family of sets
• Fuzzy set up
• Internal gear up
• Mereology
• Multiset
• Principia Mathematica
• Crude set

Notes [edit]

1. ^ ^{a b} Cantor, Georg; Jourdain, Philip E.B. (Translator) (1895). "beiträge zur begründung der transfiniten Mengenlehre" [contributions to the founding of the theory of transfinite numbers]. Mathematische Annalen (in German). New York Dover Publications (1954 English translation). xlvi, xlix: 481–512, 207–246. By an aggregate (Menge) we are to understand whatever collection into a whole (Zusammenfassung zu einem Gansen) Thou of definite and separate objects m (p.85)
2. ^ P. K. Jain; Khalil Ahmad; Om P. Ahuja (1995). Functional Analysis. New Age International. p. i. ISBN978-81-224-0801-0.
3. ^ Samuel Goldberg (1 January 1986). Probability: An Introduction. Courier Corporation. p. ii. ISBN978-0-486-65252-8.
4. ^ Thomas H. Cormen; Charles E Leiserson; Ronald L Rivest; Clifford Stein (2001). Introduction To Algorithms. MIT Press. p. 1070. ISBN978-0-262-03293-three.
5. ^ ^{a b c} Halmos 1960, p. 1.
6. ^ ^{a b} Stoll, Robert (1974). Sets, Logic and Evident Theories . W. H. Freeman and Company. pp. 5. ISBN9780716704577.
7. ^ José Ferreirós (16 August 2007). Labyrinth of Idea: A History of Set Theory and Its Office in Modernistic Mathematics. Birkhäuser Basel. ISBN978-3-7643-8349-vii.
8. ^ Steve Russ (nine December 2004). The Mathematical Works of Bernard Bolzano. OUP Oxford. ISBN978-0-xix-151370-1.
9. ^ William Ewald; William Bragg Ewald (1996). From Kant to Hilbert Volume 1: A Source Book in the Foundations of Mathematics. OUP Oxford. p. 249. ISBN978-0-19-850535-viii.
10. ^ Paul Rusnock; Jan Sebestík (25 Apr 2019). Bernard Bolzano: His Life and Work. OUP Oxford. p. 430. ISBN978-0-19-255683-vii.
11. ^ Bertrand Russell (1903) The Principles of Mathematics, chapter VI: Classes
12. ^ ^{a b} Halmos 1960, p. 2.
13. ^ Jose Ferreiros (ane November 2001). Labyrinth of Thought: A History of Set Theory and Its Role in Mod Mathematics. Springer Science & Business organisation Media. ISBN978-3-7643-5749-8.
14. ^ Seymor Lipschutz; Marc Lipson (22 June 1997). Schaum's Outline of Detached Mathematics. McGraw Hill Professional person. p. 1. ISBN978-0-07-136841-4.
15. ^ ^{a b c} "Introduction to Sets". world wide web.mathsisfun.com . Retrieved 2020-08-nineteen .
16. ^ Charles Roberts (24 June 2009). Introduction to Mathematical Proofs: A Transition. CRC Press. p. 45. ISBN978-1-4200-6956-three.
17. ^ David Johnson; David B. Johnson; Thomas A. Mowry (June 2004). Finite Mathematics: Practical Applications (Docutech Version). W. H. Freeman. p. 220. ISBN978-0-7167-6297-3.
18. ^ Ignacio Bello; Anton Kaul; Jack R. Britton (29 January 2013). Topics in Gimmicky Mathematics. Cengage Learning. p. 47. ISBN978-1-133-10742-2.
19. ^ Susanna S. Epp (four August 2010). Discrete Mathematics with Applications. Cengage Learning. p. 13. ISBN978-0-495-39132-6.
20. ^ Stephen B. Maurer; Anthony Ralston (21 January 2005). Discrete Algorithmic Mathematics. CRC Press. p. 11. ISBN978-i-4398-6375-6.
21. ^ D. Van Dalen; H. C. Doets; H. De Swart (9 May 2014). Sets: Naïve, Axiomatic and Applied: A Basic Compendium with Exercises for Use in Prepare Theory for Non Logicians, Working and Teaching Mathematicians and Students. Elsevier Science. p. 1. ISBN978-1-4831-5039-0.
22. ^ Alfred Basta; Stephan DeLong; Nadine Basta (1 January 2013). Mathematics for Information technology. Cengage Learning. p. 3. ISBN978-1-285-60843-three.
23. ^ Laura Bracken; Ed Miller (15 February 2013). Elementary Algebra. Cengage Learning. p. 36. ISBN978-0-618-95134-5.
24. ^ Halmos 1960, p. iv.
25. ^ ^{a b c} Frank Ruda (6 October 2011). Hegel's Rabble: An Investigation into Hegel's Philosophy of Right. Bloomsbury Publishing. p. 151. ISBN978-one-4411-7413-0.
26. ^ ^{a b c d eastward} John F. Lucas (1990). Introduction to Abstract Mathematics. Rowman & Littlefield. p. 108. ISBN978-0-912675-73-2.
27. ^ Weisstein, Eric Due west. "Gear up". mathworld.wolfram.com . Retrieved 2020-08-19 .
28. ^ Ralph C. Steinlage (1987). College Algebra. West Publishing Company. ISBN978-0-314-29531-6.
29. ^ ^{a b} Marek Capinski; Peter E. Kopp (2004). Measure, Integral and Probability. Springer Scientific discipline & Business Media. p. 2. ISBN978-1-85233-781-0.
30. ^ "Set Symbols". www.mathsisfun.com . Retrieved 2020-08-19 .
31. ^ ^{a b} Halmos 1960, p. 8.
32. ^ K.T. Leung; Doris Lai-chue Chen (ane July 1992). Uncomplicated Prepare Theory, Part I/2. Hong Kong Academy Press. p. 27. ISBN978-962-209-026-2.
33. ^ Aggarwal, M.L. (2021). "1. Sets". Understanding ISC Mathematics Class 11. Vol. 1. Arya Publications (Avichal Publishing Company). p. A=iii.
34. ^ Sourendra Nath, De (January 2015). "Unit-1 Sets and Functions: 1. Set Theory". Chhaya Ganit (Ekadash Shreni). Scholar Books Pvt. Ltd. p. 5.
35. ^ Halmos 1960, Sect.2.
36. ^ ^{a b} Felix Hausdorff (2005). Fix Theory. American Mathematical Soc. p. 30. ISBN978-0-8218-3835-8.
37. ^ Peter Comninos (half-dozen April 2010). Mathematical and Computer Programming Techniques for Reckoner Graphics. Springer Scientific discipline & Business organization Media. p. 7. ISBN978-1-84628-292-viii.
38. ^ ^{a b} Halmos 1960, p. 3.
39. ^ ^{a b c d e f} George Tourlakis (thirteen Feb 2003). Lectures in Logic and Set Theory: Volume ii, Set Theory. Cambridge University Press. p. 137. ISBN978-ane-139-43943-v.
40. ^ Yiannis N. Moschovakis (1994). Notes on Set Theory. Springer Scientific discipline & Business Media. ISBN978-3-540-94180-4.
41. ^ Arthur Charles Flake (2001). Formal Models of Computation: The Ultimate Limits of Computing. World Scientific. p. 3. ISBN978-981-02-4500-9.
42. ^ William Johnston (25 September 2015). The Lebesgue Integral for Undergraduates. The Mathematical Association of America. p. 7. ISBN978-1-939512-07-nine.
43. ^ Karl J. Smith (7 January 2008). Mathematics: Its Power and Utility. Cengage Learning. p. 401. ISBN978-0-495-38913-2.
44. ^ John Stillwell (xvi October 2013). The Real Numbers: An Introduction to Set Theory and Analysis. Springer Science & Concern Media. ISBN978-3-319-01577-iv.
45. ^ David Tall (eleven Apr 2006). Avant-garde Mathematical Thinking. Springer Science & Business Media. p. 211. ISBN978-0-306-47203-9.
46. ^ Cantor, Georg (1878). "Ein Beitrag zur Mannigfaltigkeitslehre". Periodical für die Reine und Angewandte Mathematik. 1878 (84): 242–258. doi:x.1515/crll.1878.84.242.
47. ^ Cohen, Paul J. (Dec 15, 1963). "The Independence of the Continuum Hypothesis". Proceedings of the National Academy of Sciences of the United states of America. 50 (6): 1143–1148. Bibcode:1963PNAS...50.1143C. doi:10.1073/pnas.50.6.1143. JSTOR 71858. PMC221287. PMID 16578557.
48. ^ Halmos 1960, p. 19.
49. ^ Halmos 1960, p. 20.
50. ^ Edward B. Burger; Michael Starbird (18 August 2004). The Heart of Mathematics: An invitation to effective thinking. Springer Scientific discipline & Business Media. p. 183. ISBN978-1-931914-41-3.
51. ^ Toufik Mansour (27 July 2012). Combinatorics of Set Partitions. CRC Printing. ISBN978-1-4398-6333-six.
52. ^ Halmos 1960, p. 28.

References [edit]

• Dauben, Joseph Due west. (1979). Georg Cantor: His Mathematics and Philosophy of the Space . Boston: Harvard University Press. ISBN0-691-02447-two.
• Halmos, Paul R. (1960). Naive Ready Theory . Princeton, North.J.: Van Nostrand. ISBN0-387-90092-vi.
• Stoll, Robert R. (1979). Set Theory and Logic. Mineola, N.Y.: Dover Publications. ISBN0-486-63829-4.
• Velleman, Daniel (2006). How To Prove It: A Structured Approach. Cambridge University Printing. ISBN0-521-67599-5.

External links [edit]

• The lexicon definition of set at Wiktionary
• Cantor's "Beiträge zur Begründung der transfiniten Mengenlehre" (in High german)

burnettedonts1968.blogspot.com

Source: https://en.wikipedia.org/wiki/Set_(mathematics)

Share this post